在外力作用下,物体的大小和形状都要发生变化,通常称之为形变。如果外力撤消后,物体能恢复原状,则这种性质称为物体的弹性;如果外力撤消后,物体不能恢复原状,则这种性质就称为物体的塑性。自然界既不存在完全弹性的物体,也不存在完全塑性的物体。对于任何物体,当外力小时,形变也小,外力撤消后,物体可完全复原;当外力大时,形变也大。若外力过大,形变超过一定限度,物体就不会复原了。这就说明,物体有一定的弹性限度,超过这个限度就变成塑性。与压电有关的问题,都属于弹性限度范围内的问题。因此,这里仅讨论石英晶振晶体的弹性性质。

一、应力

选两根长度相等,粗细不同的橡皮绳,当这两根橡皮绳受到相同的拉力作用时,显然,细橡皮绳比粗橡皮绳拉得长一些。为什么在相同的外力作用下,它们的伸长量不一样呢?这是因为两根橡皮绳的粗细不一样,也就是横截面的大小不样。由此可见,在拉力的作用下,物体的伸长量不仅与力的大小有关,而且还与石英晶振,贴片晶振等物体的横截面的大小有关。为了计入横截面大小的影响,引入单位面积的作用力(即应力)这个概念,它的数学表达式为:

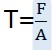
式中,T为应力,F为作用力,A为横截面(即力的作用面积)。通常规定作用力为拉力时,T>0,作用力为压力时,T<0。

二、应变

选择两根长度不等,但粗细相同的橡皮绳,当这两根橡皮绳受到相同的拉力作用时,它们的应力相同,而伸长量不同,即长橡皮绳比短橡皮绳拉得长一些。由此可见,石英晶体振荡器,石英晶振,物体的伸长量不仅与应力有关,而且还与原来的长度有关。为了计入长度的影响,引入单位长度的伸长量(即应变)这个概念。它的数学表达式为

式中,S为应变,l为原长,△l为伸长量,△l为单位长度的伸长量(或相对伸长量)。

三、正应力与正应变

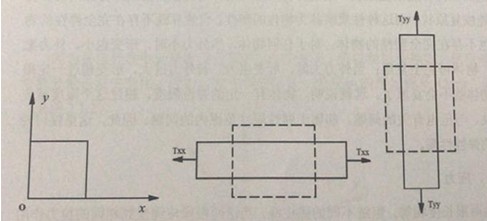
如图2.2.1(a)所示的小方片,当它受到x方向的应力作用时,除在x方向产生伸长外,同时在y方向也产生收缩,如图2.2.1(b)所示。同样,当小方片受到y方向的应力作用时,除了在y方向产生伸长外,同时在x方向也产生收缩

如图2.2.1(c)所示。上述

 (a)未受力情况(b)沿x方向受力时的形变情况(c)沿y方向受力时的形变情况

图2.2.1小方片应力、应变示意图

沿x方向应力和y方向应力的特点是,石英晶振力的方向与作用面垂直(或力的方向与作用面的法线方向平行)。为了反应这两个方向在应力符号上要附加两个足标,例如Tx和Ty。应力的第一个足标表示力的方向,第二个足标表示作用面的法线方向。同理,石英贴片晶振应变也有两个足标,例如Sx和Sy应变的第一个足标表示原长度的方向,第二个足标表示伸长量的方向,Tx、Ty又称正应力(或伸缩应力),Sx、Sy又称为正应变(或伸缩应变)为了简便,通常将足标中的(x,y,z)用(1,2,3)表示,而且将双足标简化为单足标,双足标与单足标的关系如表2.2.1所示。

四、切应力与切应变

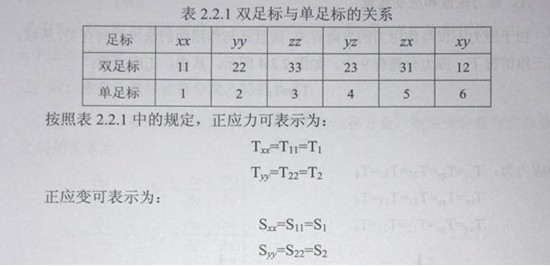
形变前为一正方形的薄片,在形变后变为菱形,这样的形变称为切变,如图22.2所示。从图中看出,切变的特点是形变前、后四个边之间的夹角发生了变化,一个对角线被拉长,另一个对角线被压缩。而且角度6xy和eyx的变化越大,切变越大。因此切应变与这两个角度之间的关系为：

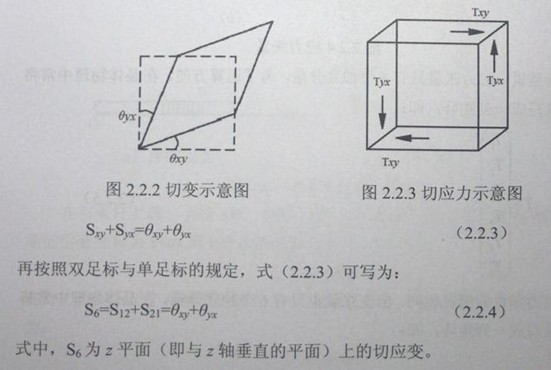
显然,S6这种切应变,在如图2.2.3所示的两对应力(Tyx,Tyx和Txy,Tyx)的作用下产生的,而这两对应力称为切应力。石英晶振切应力的特点是:力的方向与作用面平行,它可以使物体产生切变,而不能使物体产生转动,故有:

T_yx= T_xy = T₂₁ = T₁₂ =T₆